Theory of corresponding squares
1.Introduction to coordinated squares
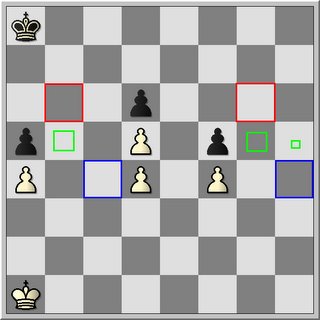
I. Consider the following position

Identify the key squares and determine which squares can be used as invasion points.

For white we have 3 key squares, in this overall blocked pawn position. If white can stand on one of these squares the opponent's pawn will irrevocable fall.
Determine the access square(s) to the key squares and draw the shortest road between the access squares for both kings.

The blue rectangles refer to the access squares of white. The blue line corresponds to the shortest road between the blue access squares.
The red rectangles on the other hand refers to black's access squares. The red line to the shortest path for black.
Configuration of path from Q-side to K-side - blue - 1,1,2,2,1,1
Configuration of path from Q-side to K-side - red - 1,1,2,2,2,1
It is important to note that black has no key squares to the Q-side only to the K-side. This is of fundamental importance. This means that black can only try to invade the position of white on the K-side but not on the Q-side. So it is essential for white to move the play to the Q-side.
Both paths are as long to each other. Each 6 moves long although the pattern is different. Black cannot take advantage of this as he has only one invasion point which does not give him room enough to invade.
On the shortest path both kings are in knight configuration to each other meaning one file difference on the correspondence square (one file distance to the distant or close opposition square). So it is vital for white if he wants to invade to take the opposition anywhere on the shortest path. Black's should always be to the left of white's king. This is the first determinant.
One access sqaure on the kingside (blue and/or red) can defend two key squares.
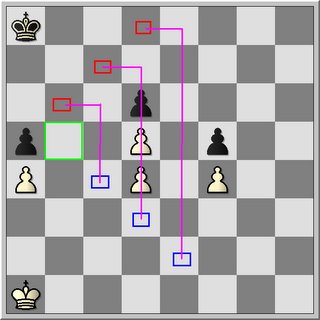
How to determine the correspondance squares
- start with the squares on the shortest path: The squares are special squares, anologous to no others on the board (yuri averbakh)
- designate a number to the squares where there is only one anologous.
- establish the relation between these opposing squares geometrically. This established relation determines what kinfd of relation we have.
- work down rank by rank
- use direct opposition to find correspondance squares
- check distance to the invasion points if the correspondance is unique.
Remember the squares on the shortest path are unique!! You need the opposition to invade.
To number the squares, go rank by rank and use direct opposition, king relation and distance to invasion point.
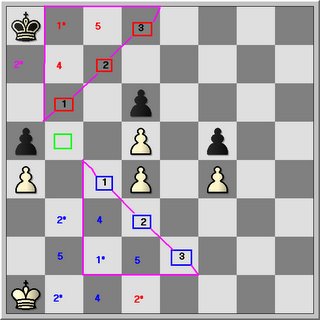
Notice that the relation 2* (red versus pink) are not always co-ordinates in true since of the meaning. Their distance are different to both invasion points and cannot be considered as real correspondance squares!! also they violate the kings' relationship to each other. (distant and one side = extended knight opposition)
I. Consider the following position

Identify the key squares and determine which squares can be used as invasion points.

For white we have 3 key squares, in this overall blocked pawn position. If white can stand on one of these squares the opponent's pawn will irrevocable fall.
Determine the access square(s) to the key squares and draw the shortest road between the access squares for both kings.

The blue rectangles refer to the access squares of white. The blue line corresponds to the shortest road between the blue access squares.
The red rectangles on the other hand refers to black's access squares. The red line to the shortest path for black.
Configuration of path from Q-side to K-side - blue - 1,1,2,2,1,1
Configuration of path from Q-side to K-side - red - 1,1,2,2,2,1
It is important to note that black has no key squares to the Q-side only to the K-side. This is of fundamental importance. This means that black can only try to invade the position of white on the K-side but not on the Q-side. So it is essential for white to move the play to the Q-side.
Both paths are as long to each other. Each 6 moves long although the pattern is different. Black cannot take advantage of this as he has only one invasion point which does not give him room enough to invade.
On the shortest path both kings are in knight configuration to each other meaning one file difference on the correspondence square (one file distance to the distant or close opposition square). So it is vital for white if he wants to invade to take the opposition anywhere on the shortest path. Black's should always be to the left of white's king. This is the first determinant.
One access sqaure on the kingside (blue and/or red) can defend two key squares.

How to determine the correspondance squares
- start with the squares on the shortest path: The squares are special squares, anologous to no others on the board (yuri averbakh)
- designate a number to the squares where there is only one anologous.
- establish the relation between these opposing squares geometrically. This established relation determines what kinfd of relation we have.
- work down rank by rank
- use direct opposition to find correspondance squares
- check distance to the invasion points if the correspondance is unique.
Remember the squares on the shortest path are unique!! You need the opposition to invade.

To number the squares, go rank by rank and use direct opposition, king relation and distance to invasion point.

Notice that the relation 2* (red versus pink) are not always co-ordinates in true since of the meaning. Their distance are different to both invasion points and cannot be considered as real correspondance squares!! also they violate the kings' relationship to each other. (distant and one side = extended knight opposition)

